Simulated Annealing

以前欠下的算法还是要学的,因为 CTF 误打误撞知道了模拟退火(Simulated Annealing,SA),对 Nano"要用魔法打败魔法,要用随机打败随机"的思路感到惊奇的同时也了解了一下这个利用随机寻找最优解的算法.

Overview

模拟退火属于一种概率算法,常用来在一定时间内寻找在一个很大搜寻空间中的近似最优解,且由于算法中引入了一些随机量,所以有很大的概率能获得全局最优解。

用一句话的来说,模拟退火算法即：如果新状态的解更优则修改答案,否则以一定概率接受新状态。

Step

模拟退火的过程一般有三个参数,初始温度 $ T_0 $ ,降温系数 $ d $ ,以及终止温度 $ T_k $ ,其中 $ 0 < d < 1, d \rightarrow 1 $ 并且 $ T_k > 0, T_k \rightarrow 0 $ .

定义好初始值以及算法的迭代起始点 $ x $ 以及对应的目标函数值 $ f(x) $ .
以一定的随机策略产生一个新的解 $ \tilde{x} $ ,并计算目标函数值 $ f(\tilde{x}) $ 和增量 $ \Delta = f(\tilde{x}) - f(x) $ .此处以求解 $ f(x) $ 最小值为例.
以某种算法决定保留当前的最优解的概率并进行保留.这是SA算法的核心部分.
若 $ T < T_k $ 时停止迭代,跳出循环.若 $ T \ge T_k $ 时用新的解替代当前的解,更新温度,函数值等,进行下一轮的迭代.

一般情况下,以 Metropolis 准则来判断解是否被接受,即当现在的情况比原来更好 $ (\Delta < 0) $ 时接受新的解,否则如果新的状态更坏 $ (\Delta > 0) $ 时以一定的概率 $ exp(\frac{-\Delta}{T}) $ 接受它,防止陷入局部最优解导致无法跳出.
其中 $ T $ 为进行判断时候的温度,当刚刚开始时, $ T $ 很大,接受概率几乎为 $ 100\% $ ,算法的行为更趋向于全局搜索,随着 $ T $ 的下降,解跳出的概率下降,因此后期更趋向于局部最优解.

可以看出,在算法的过程中怎样取得下一个新解和如何评价一个解的优劣性是将该算法推广的难点所在.

Usage

Normal Problem

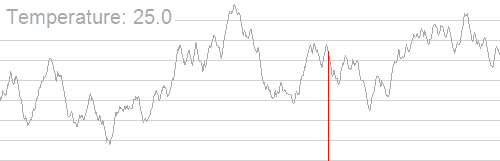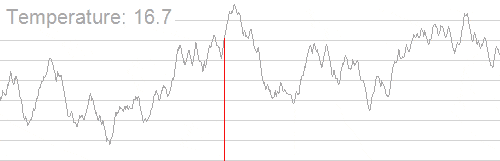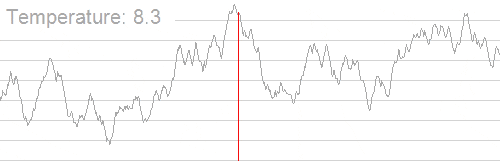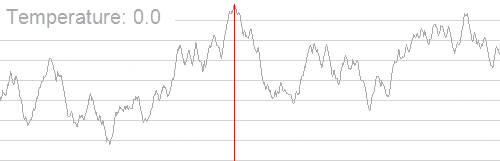
下图来自于 Wikipedia ,在搜索最高峰的过程中使用了模拟退火算法.可以看出的是,随着温度的不断降低,跳跃过程渐渐由随机趋于稳定,最优解也越来越确定.

模拟退火也是用于求解 TSP 问题的算法之一, TSP 问题即 Travelling salesman problem ,旅行商问题,也即最短路径问题: 给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。它是组合优化中的一个 NP 困难问题,在运筹学和理论计算机科学中非常重要。

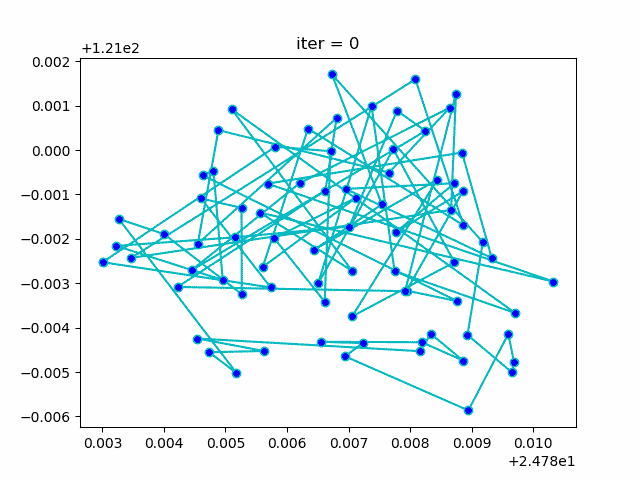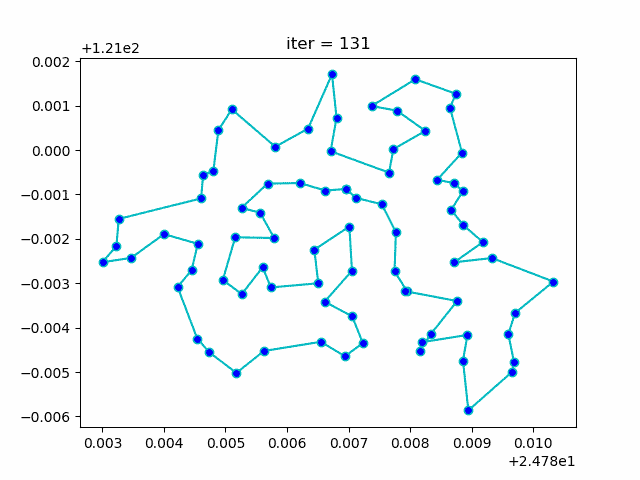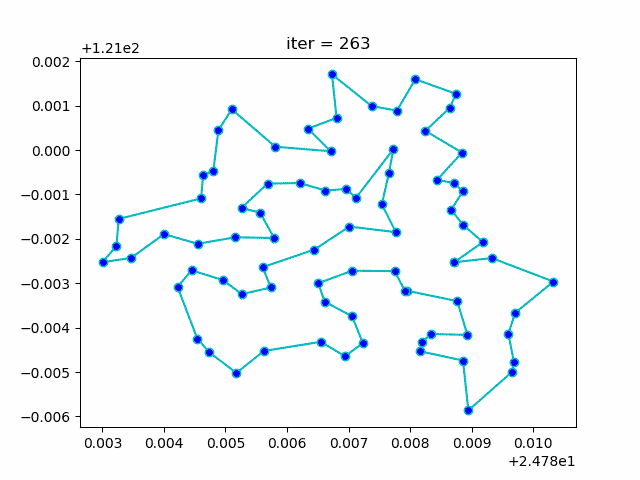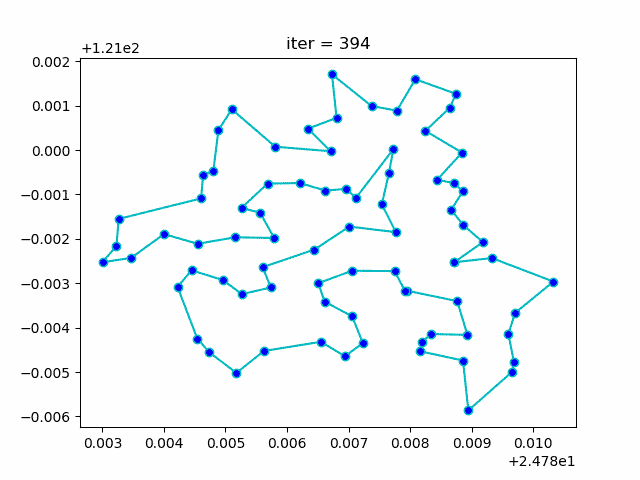
下图形象展示了利用模拟退火算法迭代计算过程中的最优解的变化情况.

Hackergame2020 - Shuffle Code

下面我将以 Hackergame2020 中的"证验码"一题中 NanoApe 给出的解法解法作为例子以探寻模拟退火算法使用的一些思路.

先讲述一下问题,题目给出了一个验证码图片的生成方法,但是在获取结果的时候,将给出一个被随机打乱像素分布的验证码,要求是给出验证码中各个字符的个数以获取 flag .

如 Code 为 P7UMsaNGG4RktOFI 时,原图片:

而被打乱的图片是这样:

(此处的图片进行了压缩,并不可以直接用于程序的计算)

图片生成代码

题目中给出了一定的提示,这道题需要利用像素点的统计特征进行推测原图的字母.这里使用NanoApe的思路:

目标是从目前的已知图片的像素中找出一种统计规律可以逆向推断出原始字母的数量.但考虑到 noise 的存在,直接的统计一定存在偏差,那么如何去除 noise 的影响便是下一个需要着重考虑的问题.

首先,在无 noise 的图像中纯灰度像素 $ (i,i,i) $ 的分布是和字母的数量种类有关的.而当时本人做这道题时候思路仅考虑了纯黑和纯白,这样是不够完善的.

进行下一步工作之前,我们需要统计一遍没有 noise 的图的每个字在图上的纯灰度像素的数量情况.

def get_feature(pic):
    feature = np.zeros(256, dtype=int)
    pix = np.array(pic)
    for x in pix.reshape(-1, pix.shape[2]).tolist():
        if (x[0], x[1]) == (x[1], x[2]):
            feature[x[0]] += 1
    return feature

feature = np.zeros((len(alphabet), 256), dtype=int)
for idx, ch in enumerate(alphabet):
    feature[idx] = get_feature(generate_captcha(ch))

并准备好目标图片的feature:

f_o = get_feature(Image.open('captcha_shuffled.bmp'))

考虑到无 noise 的图像的颜色像素中纯灰度像素 $ (i,i,i) $ 的数量都会比有 noise 的图像的分布要多,所以可以这样设置一个函数来作为评价函数,这也是算法的核心所在：

$ $ F(N,G)=\sum_{i=0}^{255}\left(\max(0,N_i-G_i)^2\times 10000+\max(0,G_i-N_i)\right) $ $

其中 $ N_i $ 表示有 noise 的图像中像素 $ (i,i,i) $ 的数量, $ G_i $ 表示无 noise 的图像中像素 $ (i,i,i) $ 的数量。

如果某个纯灰度像素在减去某一 code 对应无 noise 的图像的对应像素数量后仍然有剩余的话,证明这个 code 大概率不是目标,于是将其最大值平方后乘以 10000 以使得评价函数值变大排除这一情况.

但如果相反,那么这个差距则可以作为用于评价结果接近程度的指标,将其取最大值后累加.

于是,在获取的目标特征数组 f_o 上减去猜测的某个 code 的每一位对应的 feature 之后就可以很轻松地实现这个 score 函数:

def score(code):
    f = f_o.copy()
    for ch in code:
        f -= feature[alphabet.index(ch)]
    return np.sum(np.power(np.maximum(f, 0), 2)) * 10000 - np.sum(np.minimum(f, 0))

则此时的目标便转换为寻找 code 使得 $ F $ 最小化.这里就可以使用模拟退火的思想了.

首先初始化随机 code:

best = ''.join([random.choice(alphabet) for _ in range(16)])
best_score = score(best)

而后的过程就是,每次取 2 位 1 位和 0 位随机进行替换,这样的三次退火下每个迭代 10000 次,并保存最优的结果:

for i in range(2, 0, -1):
    for _ in range(10000):
        new = ''.join(random.sample(best, 16-i)) + ''.join([random.choice(alphabet) for _ in range(i)])
        new_score = score(new)
        if new_score < best_score:
            best, best_score = new, new_score
    print(best, best_score)

当最后的best_score小于10000时,则基本上可以确定为最优解了.

说起来这道题还有人跑了深度学习的模型,而 NanoApe 的这个算法可以在几秒钟之内得到最终结果,正确概率也很高.思想是一方面,代码实现层面的方法也有不少值得学习的地方.使我受益良多.

Summary

总的来说,模拟退火的应用范围之广也在于它的思想的价值远大于一串既定写死的代码.我认为,能将其推广,能找出对应与问题的评价函数和随机方法,并将其灵活的进行使用才是学习这个算法思想的最重要意义所在.

模拟退火(Simulated Annealing)算法